기수 정렬

기수 정렬이란?

이미지 출처 : https://herong.tistory.com/m/190?category=818669

기수 정렬 (Radix Sort)는 자리수를 비교하며 정렬을 진행하는 알고리즘 이다.

1. LSD (Least Significant Digit) 방식의 정렬

• 가장 작은 자릿수부터 정렬을 진행 (숫자로 치면 일의 자리수부터)
• 가장 작은 자릿수부터 큰 자릿수까지 비교해야 한다는 단점이 있지만, 코드 구현이 MSD에 비해 간결하다

2. MSD (Most Significant Digit) 방식의 정렬

• 가장 큰 자릿수부터 정렬을 진행
• LSD와 비교했을 때 정렬 상태 확인등의 추가 작업이 필요하지만, 중간에 정렬이 완료될 수 있다는 장점이 있다

기수 정렬의 과정

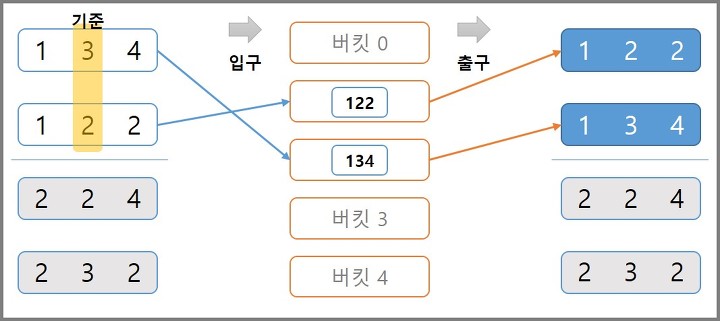
기수 정렬의 과정을 배열 [134,224,232,122] 을 정렬해보며 설명한다.

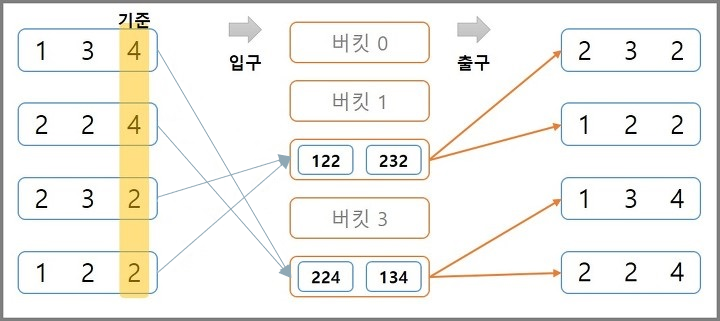
1. LSD 방식

<STEP 1>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

• 일의 자릿수부터 확인한다
• 숫자를 나타내는 버킷에 일의 자릿수를 확인하며 저장한다
• 꺼낼 때는 먼저 저장된 값부터 꺼내게 된다 (FIFO)

<STEP 2>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

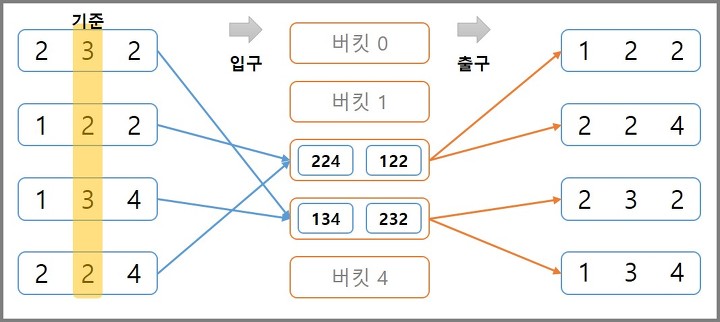
• 그 다음 자리수인 십의 자리를 기준으로 버킷에 저장한다
• 위의 과정과 동일하게 진행한다

<STEP 3>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

• 그 다음 자리수인 백의 자리를 기준으로 버킷에 저장한다
• 마지막 자리수까지 검사를 마친 경우 오름차순으로 정렬이 완료된다

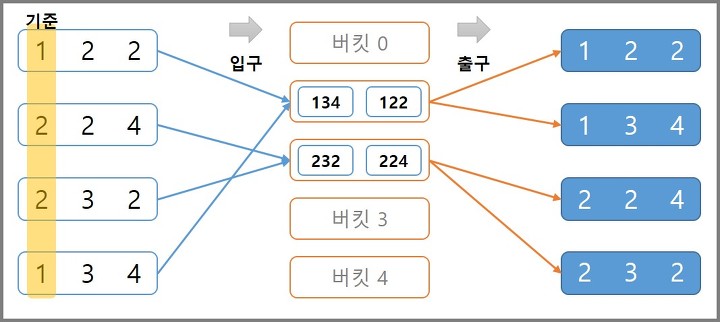
2. MSD 방식

<STEP 1>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

• 가장 큰 자릿수 (여기서는 백의 자리)부터 확인한다
• 각 숫자를 나타내는 버킷에 백의 자릿수를 확인하며 저장한다
• 꺼낼 때는 먼저 저장된 값부터 꺼내게 된다 (FIFO)

<STEP 2>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

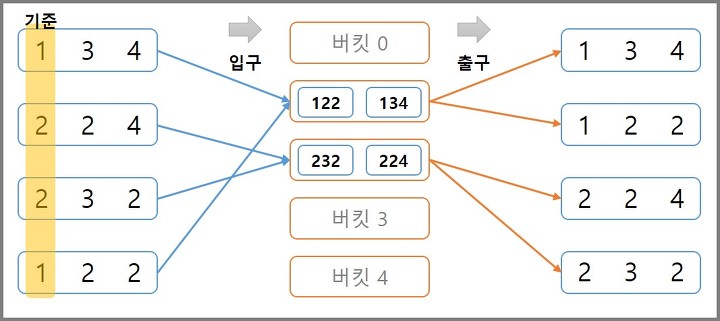
• 두번째 과정부터는 STEP 1로 분류된 그룹끼리 정렬을 수행한다
  
  

  (134,122) , (224,232)

<STEP 3>

이미지 출처 : https://herong.tistory.com/m/190?category=818669

• 두번째 그룹 (224,232)의 경우 자리수를 비교하지 않아도 이전에 정렬이 완료된 상태이므로 더 이상 정렬을 진행하지 않아도 된다

기수 정렬의 특징

• 정렬 순서상 앞과 뒤의 판단을 위한 비교 연산을 하지 않는다
• 정렬 대상의 모든 길이가 동일해야 가장 효율적이다
  
  

  좋은 예시) [123,456,789,961], [blue,fire,jong,mfam]
  나쁜 예시) [4562,12,651,-1123],[mfam,cs,study]

• 정렬 대상의 자리수를 기준으로 '버킷'이라는 공간에 '큐(Queue)' 방식으로 저장 후 다시 꺼낸다
• 같은 수의 순서가 섞이지 않는 안정 정렬이다 (MSD 방식은 불안정 정렬)

시간복잡도

• 키의 수를 $n$, 키의 최대 길이를 $d$라고 했을 때, 시간복잡도는 $O(d*n)$ 이다.

공간 복잡도

• LSD 방식의 경우 키의 수를 $n$, 버켓의 종류 수를 $k$라고 했을 때, 공간복잡도는 $O(n+k)$ 이다.
• MSD 방식의 경우 키의 수를 $n$, 버켓의 종류 수를 $k$, 키의 최대 길이를 $d$라고 했을 때, 공간복잡도는 $O(n+d*k)$ 이다.

---

코드로 구현한 기수 정렬

c++

void Radix_Sort()                // 기수정렬 함수 !
{
    int Radix = 1;                // 최대 자릿수까지 계산을 하기 위한 변수
    while (1)                    // 최대 자릿수가 몇 자리인지 알아내기 위한 반복문 !
    {
        if (Radix >= Max_Value) break;    // Max_Value는 입력과 동시에 구해놓은 배열에서의 최댓값 !
        Radix = Radix * 10;        
    }
    for (int i = 1; i < Radix; i = i * 10)    // 1의 자리부터 10씩 곱하면서 최대자릿수 까지 반복 !
    {
        for (int j = 0; j < MAX; j++)    // 모든 배열을 다 탐색하면서
        {
            int K;
            if (Arr[j] < i) K = 0;        // 만약 현재 배열의 값이 현재 찾는 자릿수보다 작으면 0 !
            else K = (Arr[j] / i) % 10;    // 그게 아니라면 위에서 말한 공식 적용 !
            Q[K].push(Arr[j]);        // Queue배열에 해당 값을 순차적으로 저장 !
        }

        int Idx = 0;
        for (int j = 0; j < 10; j++)    // 0부터 9까지 Queue에 저장된 값들을 순차적으로 빼내기 위한 반복문.
        {
            while (Q[j].empty() == 0)    // 해당 Index번호의 Queue가 빌 때 까지 반복
            {
                Arr[Idx] = Q[j].front();    // 하나씩 빼면서 배열에 다시 저장.
                Q[j].pop();        
                Idx++;
            }
        }
    }
}

코드 출처

Java

package Sort;

import java.util.Arrays;
// 기수 정렬 알고리즘 구현
public class radix {
    // 배열에서 최대값을 얻기 위한 메서드
    static int getMax(int[] data) {
        int mx = data[0];
        for(int i=1; i<data.length; i++) {
            if(data[i] > mx) {
                mx = data[i];
            }
        }
        return mx;
    }
    // exp 변수의 수에 따라 숫자를 정렬
    static void countSort(int[] data, int exp) {
        int[] output = new int[data.length];
        int[] count = new int[10];
        Arrays.fill(count, 0);
        
        // count 값 count배열에 저장
        for(int i=0; i<data.length; i++) {
            count[(data[i]/exp)%10]++;
        }
        // count 값이 포함시켜 count배열에 저장
        for(int i=1; i<10; i++) {
            count[i] += count[i-1];
        }
        // output배열 빌드
        for(int i=data.length-1; i>=0; i--) {
            output[count[(data[i]/exp)%10]-1] = data[i];
            count[(data[i]/exp)%10]--;
        }
        // output 배열에 저장된 값을 data 배열에 저장
        for(int i=0; i<data.length; i++) {
            data[i] = output[i];
        }
    }
    static void radixsort(int[] data) {
        // 최대값 찾기
        int m = getMax(data);
        for(int exp=1; m/exp>0; exp*=10) {
            countSort(data, exp);
        }
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int [] data = {4, 54, 2, 8, 63, 7, 55, 56};
        // 기수 정렬 전
        System.out.println("# 기수 정렬 전");
        for(int i=0; i<data.length; i++) {
            System.out.print(data[i]+" ");
        }
        System.out.println();
        
        radixsort(data);
        // 기수 정렬 후
        System.out.println("# 기수 정렬 후");
        for(int i=0; i<data.length; i++) {
            System.out.print(data[i]+" ");
        }
    }

}

코드 출처

Python

def countingSort(arr, digit):
    n = len(arr)
  
    # 배열의 크기에 맞는 output 배열을 생성하고 10개의 0을 가진 count란 배열을 생성한다. 
    output = [0] * (n)
    count = [0] * (10)
    
    #digit, 자릿수에 맞는 count에 += 1을 한다. 
    for i in range(0, n):
        index = int(arr[i]/digit) 
        count[ (index)%10 ] += 1
 
    # count 배열을 수정해 digit으로 잡은 포지션을 설정한다.  
    for i in range(1,10):
        count[i] += count[i-1]  
        print(i, count[i])
    # 결과 배열, output을 설정한다. 설정된 count 배열에 맞는 부분에 arr원소를 담는다.   
    i = n - 1
    while i >= 0:
        index = int(arr[i]/digit)
        output[ count[ (index)%10 ] - 1] = arr[i]
        count[ (index)%10 ] -= 1
        i -= 1

    #arr를 결과물에 다시 재할당한다.  
    for i in range(0,len(arr)): 
        arr[i] = output[i]
 
# Method to do Radix Sort
def radixSort(arr):
    # arr 배열중에서 maxValue를 잡아서 어느 digit, 자릿수까지 반복하면 될지를 정한다. 
    maxValue = max(arr)  
    #자릿수마다 countingSorting을 시작한다. 
    digit = 1
    while int(maxValue/digit) > 0: 
        countingSort(arr,digit)
        digit *= 10
 
arr = [ 170, 45, 75, 90, 802, 24, 2, 66]
#arr = [4, 2, 1, 5, 7, 2]
radixSort(arr)
 
for i in range(len(arr)):
    print(arr[i], end=" ")

코드 출처

---

기수 정렬의 장단점

장점

• 키의 길이 $d$가 작다면 $O(n)$의 시간으로 정렬을 할 수 있기 때문에 굉장히 빠른 속도로 정렬을 할 수 있다
• 카운팅 정렬과 같이 비교 연산 없이 정렬을 수행 할 수 있다

단점

• 추가적으로 버킷을 사용하기 때문에 데이터 크기에 비례한 메모리가 필요하다
• 버킷의 종류 (2진수,10진수,알파벳) 등이 고정적이지 않다
• 정렬 방법의 특수성 때문에, 부동소수점 실수처럼 특수한 비교 연산이 필요한 데이터에는 적용하기 힘들다

면접에 나올 수 있는 질문

Q. 기수 정렬이란?

A. 버킷을 활용해서 자리수를 비교하며 정렬을 진행하는 알고리즘이다.

Q. 기수 정렬의 시간 복잡도와 공간 복잡도는?

A. 키의 개수가 $n$, 키의 최대 길이가 $d$, 버킷의 종류가 $k$라고 할 때,
시간복잡도는 $O(n*d)$이고
LSD방식의 경우 공간복잡도는 $O(n+k)$, MSD방식의 경우 공간복잡도는 $O(n+d*k)$이다.

Q. 다른 알고리즘과 비교했을 때 기수 정렬이 가지는 장점은?

A. 기수 정렬의 시간 복잡도는 $O(n*d)$로 키의 길이가 길지 않은 경우에는 굉장히 빠른 시간에 정렬이 가능하다는 장점이 있다.

참고

• 기수 정렬
• 기수정렬(Ridix Sort)
• [ch 10-2] 복잡하지만 효율적인 정렬 알고리즘_3(기수 정렬)
• MSD( Most Significant Digit ) Radix Sort

---

기여자

_Jongminfire
📦